Deep Residual Learning for Image Recognition

Highlights of ResNet Paper

• Present a residual learning framework to train very deep networks more easily.
Reformulate the layers as learning residual functions instead of learning unreferenced functions.
• Training 8x deeper networks than VGG-net
• 3.57% error on the ImageNet test set, 28% relative improvement on COCO object detection dataset.
• Topping the leader board in ILSVRC & COCO 2015 (ImageNet classification, detection, localization, COCO detection & segmentation)

Introduction

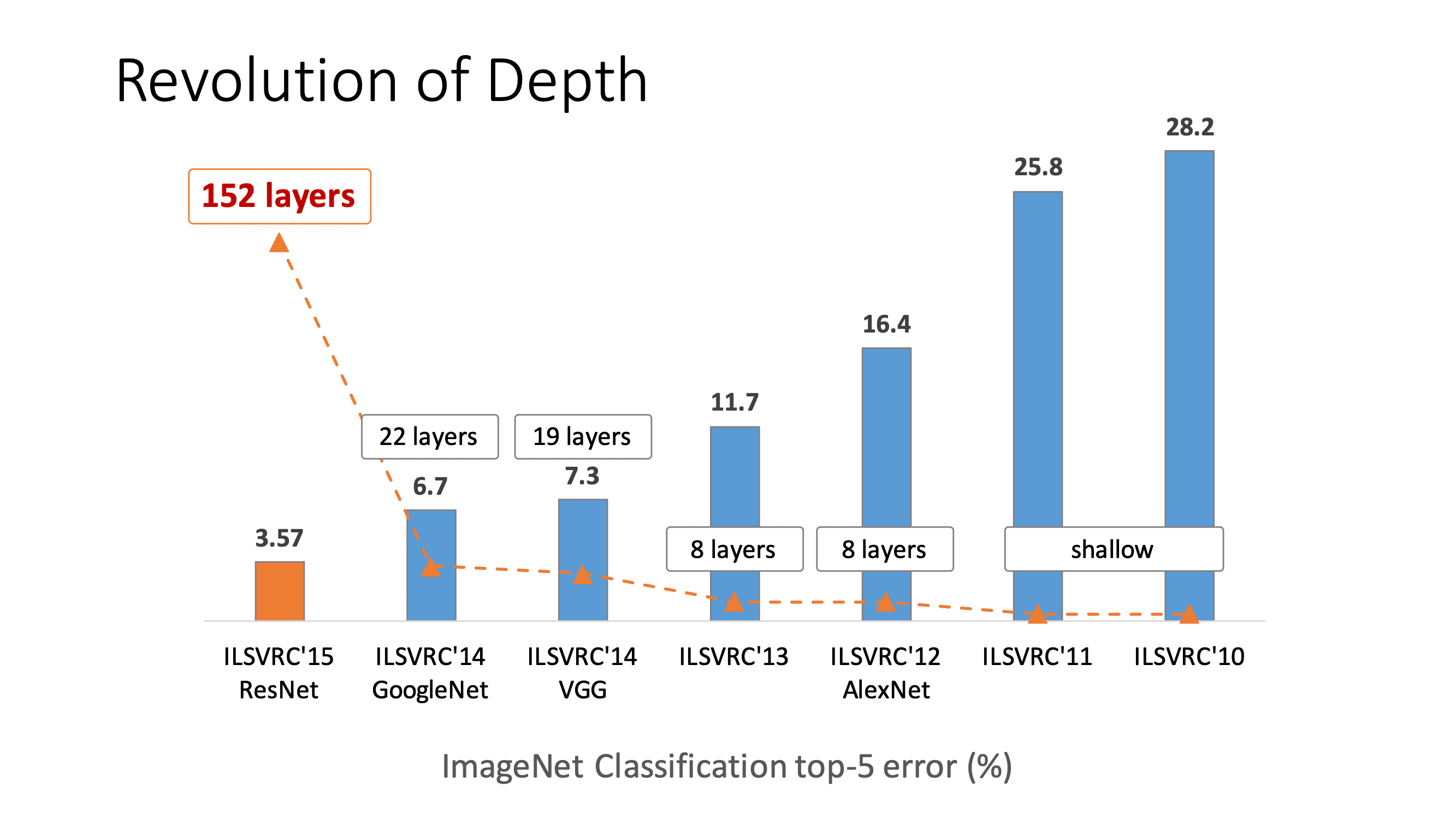
From the ImageNet Classification results in 2014-2015, it was evident that having deeper networks helps to learn greater levels of features. As shown in the figure below, we can see that VGG-Net and GoogLeNet have reduced the top-5 error rate further by having deeper networks.

So if we just stack more and more layers, does that help? Turns out it doesn't. One reason for this is the vanishing gradient problem which was studied by Sepp Hochreiter in 1991 [14] and discussed over the years [1], [8]. This problem makes it difficult for a network to converge from the start. This issue has been addressed through various initialization methods and through batch normalization [16].

Even when a network starts converging, in deeper networks, researchers have found that there is a degradation of accuracy. Particularly, when we start increasing the depth of a model the accuracy gets saturated, and then it degrades rapidly. As  evident from the learning curves, this is not due to overfitting$^{\star}$.$^{\star}$Check the left figure : Once the depth is increased by increments of 12.

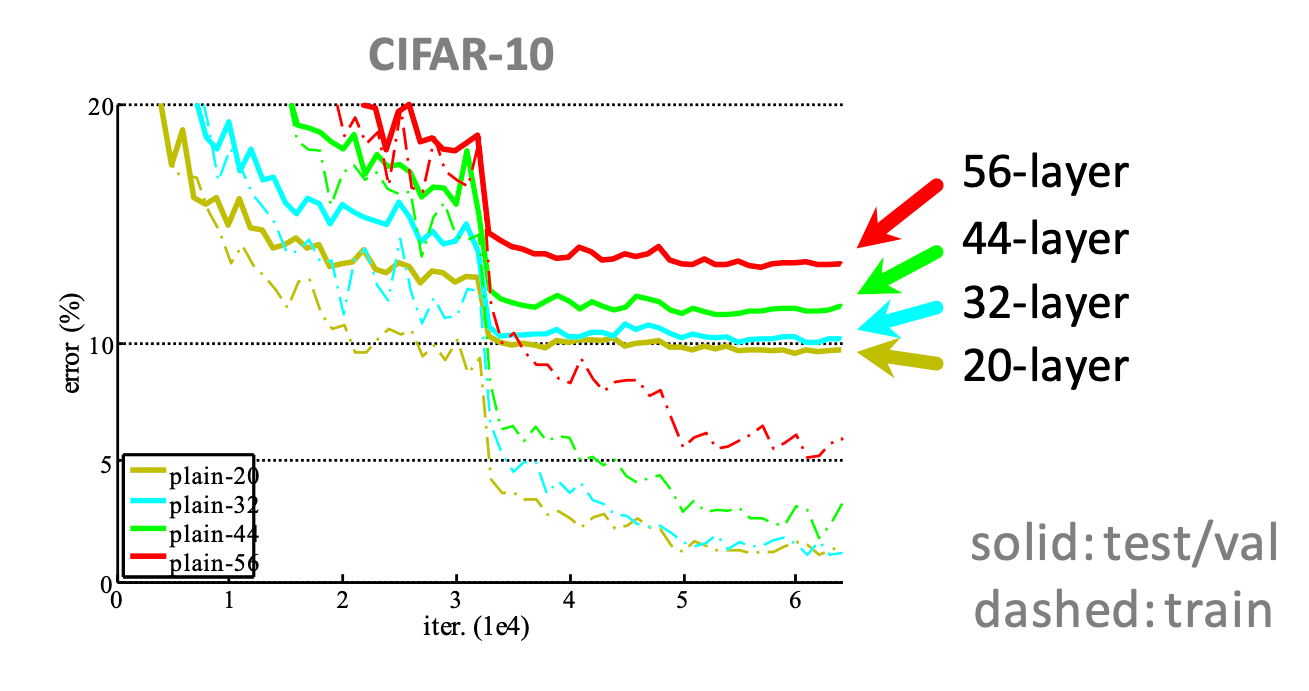
The authors of the ResNet paper argue that, even if we increase the depth, theoretically there should be solution which gives the same accuracy. So it's basically the shallow network + layers with identity transform. 💡 Why can't the added layers become an identity mapping 🤷🏻 However, the problem seems that the optimizers cannot reach that solution. So can we do a trick and get there easily? That's what authors hypothesize.

Methodology - Deep Residual Learning

Fitting a residual mapping

$\mathcal{H}$ - Mapping that needs to be fit by few stacked layers

$\mathrm{x}$ - input to the first of those layers

Let's say we need to approximate the function $\mathcal{H}$ by some set of layers of a neural network. Authors propose that, rather than learning $\mathcal{H}$ can we let the few layers approximate a residual function ( $\mathcal{H}-\mathrm{x}$ ).  🤔

Let's denote this new function by $\mathcal{F}$. So, now we have rewritten original the function we need to approximate as, $\mathcal{H}(\mathrm{x})=\mathcal{F}(\mathrm{x})+\mathrm{x}$.

Ok, so what benefit does this give?  🤷🏻

By reformulating, we saw was that, $\mathcal{H}$ was split into an addition of a function $\mathcal{F}$ with the input. In the degradation problem that we saw earlier, the issue was that learning the identity function was hard $^{\star}$. However with this residual learning reformulation, it should be easy for the optimizer to drive the weights of the layers such that $\mathcal{F}$ becomes a zero mapping.$^{\star}$Otherwise deeper networks should've learnt identity function in its deep layers, giving out similar accuracies In this way, we are left with $\mathcal{F}(\mathrm{x})+\mathrm{x}$ which is the identity mapping.