Does Bilateral Laplace Transform Exist for Sin(t) ?
This had been a question which was bothering me. So here is my question posted on DSP, Stackexchange.
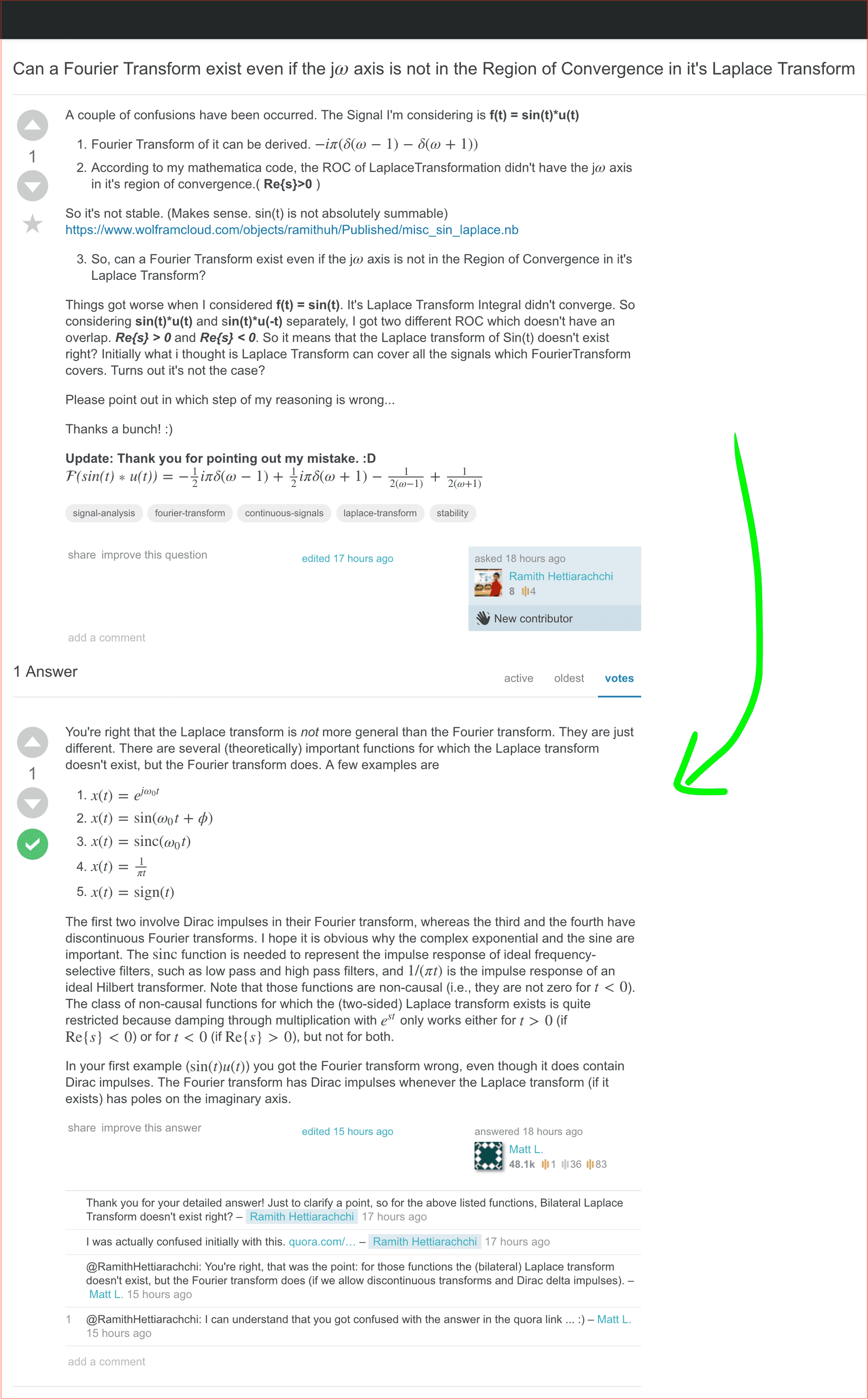
When we were learning Fourier Transforms, we easily derived the fourier transform of sin(t) using it's Fourier Series coefficients. But it appeared that the Laplace transform (bilateral) didn't converge. So then I computed the laplace transform for sin(t)*u(t).
(in other words, computing the Unilateral Laplace Transform of sin(t) )
How can it happen? Here's the expert answer..
References:
https://math.stackexchange.com/questions/1478497/unilateral-and-bilateral-laplace-transorm